
Philosophy Department
University of Waterloo
Waterloo, Ontario, N2L 3G1
pthagard@watarts.uwaterloo.ca
© Paul Thagard and Cameron Shelley, 1997
To go directly a particular section of this paper, click on a section title below.
| 1. The models |
| 2. The limitations |
| 3. Visual abduction |
| 4. The demise of SK54 |
| 5. Coherence |
| 6. Conclusion |
To return to the Coherence Articles Table of Contents page, click here.
Abstract
This paper discusses abductive reasoning---that is, reasoning in which explanatory hypotheses are formed and evaluated. First, it criticizes two recent formal logical models of abduction. An adequate formalization would have to take into account the following aspects of abduction: explanation is not deduction; hypotheses are layered; abduction is sometimes creative; hypotheses may be revolutionary; completeness is elusive; simplicity is complex; and abductive reasoning may be visual and non-sentential. Second, in order to illustrate visual aspects of hypothesis formation, the paper describes recent work on visual inference in archaeology. Third, in connection with the evaluation of explanatory hypotheses, the paper describes recent results on the computation of coherence.
There has been an explosion of recent work in artificial intelligence that recognizes the importance of abductive reasoning---that is, reasoning in which explanatory hypotheses are formed and evaluated. Many important kinds of intellectual tasks, including medical diagnosis, fault diagnosis, scientific discovery, legal reasoning, and natural language understanding have been characterized as abduction. Appropriately, attempts have been made to achieve a more exact understanding of abductive reasoning by developing formal models that can be used to analyze the computational properties of abductive reasoning and its relation to other kinds of inference. Bylander et al. [4] have used their formal model to analyze the computational complexity of abduction and show that in general it is NP-hard. Konolige [16] has used a similar formal model to derive results concerning the relation between abductive reasoning and Reiter's model of diagnosis [16]. While these formal results are interesting and useful, it would be unfortunate if researchers were to conclude that the analyses of Konolige, Bylander et al. have provided a precise understanding of abductive reasoning. We shall discuss numerous important aspects of inference to explanatory hypotheses that are not captured by one or both of the formalisms that these authors have proposed. In particular, we show how these models do not adequately capture abductive discovery using representations that are pictorial, and we argue that abductive evaluation should be conceived in terms of coherence rather than deduction.
Konolige's model of abduction is contained in two definitions:
Definition 1.1 Let L be a first order language. A simple causal theory is a tuple {C,E,Sigma} where:
1. C, a set of sentences of L, are the causes;
2. E, a set of sentences of L, are the effects;
3. Sigma, a set of sentences of L, is the domain theory.
Definition 1.2 Let {C,E,Sigma} be a simple causal theory. An explanation of a set of observations O subset E is a finite set A subset C such that:
1. A is consistent with Sigma;
2. Sigma cup A vdash O;
3. A is subset-minimal over sets satisfying the first two conditions, i.e., there is no proper subset of A consistent with Sigma that implies O.
Bylander and his colleagues offer a similar definition:
Definition 1.3 An abduction problem is a tuple {Dall,Hall,e,pl} where:
1. Dall is a finite set of all the data to be explained;
2. Hall is a finite set of all the individual hypotheses;
3. e is a map from all subsets of Hall to subsets of Dall;
4. pl is a map from subsets of Hall to a partially ordered set representing the plausibility of various hypotheses.
A set of hypotheses H is an explanation if it is complete and parsimonious, i.e., if e(H) = Dall, and no proper subset of H explains all the data that H does.
The similarities between these two sets of definitions are clear. Konolige's [16] causes correspond to Bylander et al. [4] hypotheses; Konolige's effects correspond to Bylander et al.'s data. Konolige's requirement that a set of causes be subset-minimal is the same as Bylander et al.'s requirement that a set of hypotheses be parsimonious. (Peng and Reggia [21] call the same property irredundancy.) Bylander et al. [4] go beyond Konolige in requiring an explanation to explain all the data and in adding a plausibility ordering on hypotheses. On the other hand, their definition is more general than Konolige's in not restricting data and hypotheses to sentences.
These definitions usefully capture much of what is central in abductive reasoning, particularly the goal of assembling a set of hypotheses (causes) that provide good explanations of the data (effects). But each of them oversimplifies abductive reasoning in several important respects.
First, let us consider the nature of explanation. The analysis of Bylander et al. contains the unanalyzed function e that specifies which hypotheses explain which data. Konolige's account has the apparent advantage that it spells out this relation by using the notion of logical consequence as represented by the turnstile "vdash". Hypotheses (causes) explain data (effects) if the latter can be deduced from the former and the domain theory. Konolige is thus assuming a deductive account of explanation that has been the subject of several decades of critical discussion in the philosophy of science.
In 1948, Hempel and Oppenheim proposed what has come to be known as the deductive-nomological model of explanation [12]. On this model, an explanation is a deductive argument in which a sentence representing a phenomenon to be explained is derived from a set of sentences that describe particular facts and general laws (nomos is Greek for law). This model provides a good approximation for many explanations, particularly in mathematical physics. But it is evident that the deductive model fails to provide either necessary or sufficient conditions for explanation. See [15] for a comprehensive review of several decades of philosophical discussions of the nature of explanation, and [18] for application to artificial intelligence.
First, there are many explanations in science and everyday life that do not conform to the deductive model. Hempel himself discussed at length statistical explanations in which what is explained follows only probabilistically, not deductively, from the laws and other sentences that do the explaining. Many critics have argued that explanations in such fields as history and evolutionary biology rarely have a deductive form. In both philosophy and AI, researchers have proposed that many explanations can be understood in terms of applications of schemas that fit a phenomenon into a pattern without producing a deductive argument. (For a review of different approaches to explanation in these fields, see [27, 28].) For example, a Darwinian explanation of how a species evolved by natural selection applies a general pattern that cites biological mechanisms and historical facts to suggest how an adaptation might have come about. But the historical record is too sparse and biological principles are too qualitative and imprecise for deductive derivation. Thus Konolige's use of deduction in his characterization of abduction arbitrarily excludes many domains in which hypotheses are formed and evaluated but do not provide deductive explanations.
Second, the deductive model of explanation does not even provide sufficient conditions for explanation, since there are examples that conform to the model but do not appear to constitute explanations. For example, we can deduce the height of a flagpole from information about its shadow along with trigonometry and laws of optics. But it seems odd to say that the length of a flagpole's shadow explains the flagpole's height. Konolige's subset-minimality requirement serves to rule out some of the cases of irrelevance that philosophers have discussed, for example the explanation that a man is not pregnant because he takes birth control pills. But other examples such as the flagpole show that some additional notion of causal relevance is crucial to many kinds of explanation, and there is little hope of capturing this notion using logic alone. Contrast Pearl's [20] work on Bayesian networks and Peng and Reggia's [21] model of abduction which employ ineliminably intuitive notions of causality. A general model of abduction requires an account of explanation that is richer than deduction.
Bylander et al. assume that abduction can be characterized by distinguishing sets of data from sets of hypotheses, with explanation consisting of a mapping from the latter to the former. This characterization is adequate for straightforward kinds of medical diagnosis involving a given set of symptoms (data) that can be explained by a given set of diseases. But it neglects the complexity of other kinds of abductive tasks in which the organization of hypotheses and data is more complex. In particular, it rules out a large set of cases where hypotheses explain other hypotheses and selection of the best overall explanation depends on taking these relations into account. For example, in legal inference the availability of a possible motive goes a long way to increasing the chance for a murder conviction. The data are the various pieces of physical evidence, e.g., that the suspects' fingerprints were found on the murder weapon. The hypothesis is that the suspect is the murderer, and a higher level hypothesis might be that the suspect hated the victim because of some previous altercation. The plausibility of the lower-level hypothesis comes not only from what it explains, but also from it itself being explained. This kind of hierarchical explanation in which hypotheses explain other hypotheses that explain data is also found in science and medicine; it has been discussed both in the context of Bayesian models of probabilistic belief revision [20] and in the context of explanatory coherence accounts of scientific inference [26, 28].
Just as Bylander et al. assume that only data are explained, so Konolige assumes that only observed effects are explained by derivation from causes. But as both Bayesian and explanatory coherence analyses allow, causes are often themselves effects and assessment of overall acceptability of explanatory hypotheses must take this into account.
The definitions of Konolige and Bylander et al. have the unfortunate implication that abduction is always a matter of selection from a known set of hypotheses or causes. Creative abduction often involves the construction of novel hypotheses involving newly formed concepts such as natural selection or AIDS. For Charles Peirce, who coined the term ``abduction'' a century ago, the introduction of unifying conceptions was an important part of abduction [11, 25], and it would be unfortunate if our understanding of abduction were limited to more mundane cases where hypotheses are simply assembled. Abduction does not occur in the context of a fixed language, since the formation of new hypotheses often goes hand in hand with the development of new theoretical terms such as ``atom,'' ``electron,'' ``quark,'' ``gene,'' ``neuron'' and ``AIDS.''
The first clause of Konolige's second definition requires that a hypothesized cause A be consistent with a domain theory. While this requirement may be acceptable for mundane applications, it will not do for interesting cases of belief revision where the introduction of new hypotheses leads to rejection of previously held theories. For example, when Darwin proposed the hypothesis that species evolve as the result of natural selection, he was contradicting the dominant view that species were fixed by divine creation. Konolige's consistency requirement would prevent Darwin's hypothesis from ever being considered as part of an abductive explanation that would eventually supplant the accepted biological/theological domain theory. We can not simply delete a belief and then replace it with one inconsistent with it, because until the new belief comes in competition with the old one, there is no reason to delete the old one. Belief revision requires a complex balancing of a large number of beliefs and kinds of evidence. Algorithms for performing such balancing are available, such as Bayesian belief revision and connectionist judgments of explanatory coherence. Bylander et al. do not have a consistency condition like Konolige's.
Bylander et al. do not count a set of hypotheses as an explanation unless it is complete, i.e., explains all the data. They admit that there might be ``partial'' explanations, but want completeness as a requirement because of the goal that all the data should be explained. This is a laudable goal, but does not justify building completeness into the definition of an explanation, since the goal is so rarely accomplished in realistic situations. From medicine to science, it is not typically the case that everything can be explained even by the best of theories. Even the greatest scientific theories such as Newtonian mechanics have faced anomalies through their histories; for example, the perihelion of Mercury was not explained until Einstein developed the theory of relativity. Doctors need to make diagnoses even when some symptoms remain puzzling. The requirement of completeness makes sense only in limited closed domains such as simple circuits where one can be assured that everything can be explained given the known causes.
Many researchers on abduction have seen the need to use simplicity as one of the constraints on inference to the best explanation, i.e., we want not simply a set of hypotheses that explain as much as possible, but also the most economical set of assumptions possible. Hobbs et al. [13] sum this up by saying that we want the most bang (facts explained) for the buck (quantity of assumptions). But simplicity is an elusive notion that is not adequately captured by the relation of subset minimality which deals only with cases where we can prefer an explanation by a set of hypotheses to an explanation by a superset of those hypotheses. We need a broader notion of simplicity to handle cases where the competing explanations are accomplished by sets of hypotheses that are of different sizes but are not subsets of each other. Such cases are common in the history of science and require richer notions of simplicity than subset minimality [28, 25].
Konolige's definition, like virtually all available accounts of abduction, presumes that explanatory hypotheses are represented sententially. But we will now show that some abductive inference is better understood as using pictorial or other iconic representations.
Peirce claimed that all thinking is in signs, and that signs can be icons, indices, or symbols [10, 11]. Icons are signs that resemble what they represent; examples include pictures, photographs, and geometrical diagrams. Peirce placed great emphasis on diagrammatic thinking and even developed a powerful system of predicate logic based on diagrams or ``existential graphs'' [23]. Surprisingly, Peirce does not seem to have connected his two highly original insights: we know of no text in which he discusses abduction as diagrammatic or iconic. But there are instances of abductive thinking that are most plausibly interpreted as pictorial.
Suppose you return to your car at the shopping center and find a big scratch on one door. Naturally, you wonder how it happened and start to generate hypotheses to explain how the scratch came to be. Your abductions may be purely verbal, if you start to apply rules such as ``If a car door is opened and collides with another car door, the latter door is scratched.'' You could then verbally abduce that some other car door was opened and collided with yours. But a mode of thinking that is natural for many people is to perform the same kind of thinking pictorially. You can form a mental image of a car driving up beside yours and then its driver opening a door that scratches yours. Here the explanation is a kind of mental movie in which you imagine your door being scratched. The abductive inference that the accident happened this way involves a mental picture of the other car's door hitting yours. Such pictures provide an iconic representation of the event that you conjecture to have happened, since the picture you form resembles the hypothesized event in a much more direct way than a verbal/sentential representation would. Whenever our knowledge of how things work in the world involves dynamic pictorial representations, these representations can be used to generate iconic explanations of what occurs. Many scientists have reported that images played a crucial role in their most creative thinking: the most eminent include Bohr, Boltzmann, Einstein, Faraday, Feynman, Heisenberg, Helmholtz, Herschel, Kekule, Maxwell, Poincare, Tesla, Watson, and Watt.
Performing abduction visually may have strong cognitive advantages. With verbal representations such as rules, it may be necessary to search through many possible inferences before finding a plausible explanatory hypothesis. But a picture of a situation may immediately suggest a likely cause, if it vividly displays factors that are spatially contiguous and therefore more likely to be causally relevant. Artificial intelligence is still very limited in its ability to use such visuospatial information, although progress is being made in the direction of imagistic representations. Glasgow has argued for the importance of spatial reasoning in AI and proposed a representational scheme based on 3-dimensional arrays [9, 8]. Graphs provide visual representations that are more flexible than arrays [5, 30], so to show how abduction can be visual yet nevertheless amenable to formal treatment, we will now discuss graph grammars.
A simple graph can be thought of as a purely algebraic structure consisting of a set of vertices and edges, but uses of graphs often exploit their visual character. When we draw a graph representing, for example, the paths between various cities, we get a diagram or mental representation of the routes between cities that resembles the actual roads. The mathematical structure of a graph naturally translates into a graphical diagram that resembles what it represents much more directly than a set of sentences would. Graph grammars consist of sets of production rules that differ from standard verbal productions in that the left-hand sides (conditions) and right-hand sides (actions) are represented as graphs rather than as verbal structures [7, 14, 19]. A graphical production can be interpreted as saying that if you have one graphical structure and you apply a transformation to it, then you get another graphical structure. For abduction purposes, we can think of the right-hand side of a graph production as providing a visual representation of something to be explained, and the left-hand side and the transformation as providing a possible visual explanation.
(Graphic not available)
Figure 1. Graph representation of a Lego block.
To be more concrete, consider children's interlocking Lego blocks. We can represent each block as a graph whose vertices are connectors and sockets, where the connectors on one block fit into the sockets on another block. Figure 1 gives a graph for a simple 4-connector block, with 8 vertices and 12 edges. Transformations possible for Lego blocks include stacking one on top of the other, which produces a new structure in which the connectors on the bottom block go into the sockets on the top block. A graphical production representing this would have a left-hand side of two unconnected graphs and a transformation that produced new edges connecting the appropriate sockets and connectors, producing a new connected graph with a total of 16 vertices and 28 edges, including 4 new ones.
Given such a production, we could explain the existence of a tower consisting of two blocks by hypothesizing that there were two independent blocks that had been transformed by joining. Abduction is then visual because the representations of both what gets explained and what does the explaining use structures that resemble what they represent.
Let us now state this more formally.
Definition 3.1 A graph G is a tuple {V,E} where:
- V is a set of vertices;
- E subset (V times V) is a set of edges.
Definition 3.2 A graph grammar Gamma is a finite set of productions P, where a production is a tuple {Gl,Gr,T} such that:
- Gl is the left-hand side;
- Gr is the right-hand side;
- T is the embedding transformation that specifies the relations between the vertices and edges of Gl and Gr.
Definition 3.3 A graph-grammatical abductive explanation of a target graph G^t is a hypothesis graph G^h such that there is a set of productions in P whose successive transformations transform G^h into G^t.
Intuitively, the hypothesis graph G^h provides an explanation of the target graph G^t by virtue of a series of transformations that show how the target graph can be produced from the hypothesis graph.
Graph grammars are not the only possible basis for visual abduction. Leyton [17] presented a ``process grammar'' that could be used to infer the causal history of objects from their shapes. This grammar contains such productions as one that can be interpreted: ``If a shape is squashed, it will indent.'' If the shapes and the processes of squashing and indenting are represented pictorially, then the inference that explains a shape's indentation by its having been squashed is an instance of visual abduction.
This paper does not attempt to present a general theory of visual abduction, but rather some instances that show the limitations of current formal models of abductive reasoning. A fully general characterization of abduction would have to allow representations of causes and effects that are pictorial as well as ones that are sentential. It would also have to admit forms of explanation that centrally employ visual transformations as well as ones that employ deduction and other verbal processes. In addition, we should not rule out the possibility of a multimodal theory of abduction that includes non-visual, non-verbal representations involving smell, touch, and emotion. For example, there are some diseases that physicians can diagnose based on a patient having a particular odor. The need for a multimodal theory is illustrated below with an archaeological example.
Forming hypotheses to explain the unusual macroscopic properties of artifacts and skeletal remains is an important part of archaeology. This kind of abduction often requires the archaeologist to reconstruct the events in the history of an object which caused it to change in shape or structure from some initial form to the final, observed one. Since this kind of evidence for the history of an object is visual in nature, the archaeologist may find visual mental imagery useful in generating an explanation of it. (See [24] for further discussion.

Figure 2. The skullcap SK54 with notches indicated by white arrows [2, p. 1117]

Figure 3. The abduced fate of SK54 in the jaws of a leopard [2, p. 1118]
For example, in 1949 excavations of a cave at Swartkrans in South Africa yielded, among much other debris, the skullcap of an australopithecine (thereafter designated SK54). The distinctive features of this skullcap consisted of two notches, one on either side of the centerline, which had obviously been driven into the back of the skull by two pointed objects when the creature was still alive [2]. SK54 is pictured in figure 2, with the notches indicated by the two arrows. At first it was supposed that the notches had been inflicted by two separate blows from a weapon wielded by another hominid, because each notch had been made at divergent angles from the centerline [1]. This hypothesis accorded well with the prevailing theory that human evolution had been driven by murder and cannibalism---Dart's [6] ``killer ape'' hypothesis.
However, an alternative explanation has been offered by Brain [2]. Noting that the lower canine teeth of leopards diverge and are about the right distance apart, Brain hypothesized that the notches had been created by a leopard which had taken the australopithecine's head in its mouth, as dramatically illustrated in figure 3. Indeed, a fossil leopard jaw from the same site (SK349) fits the notches fairly well and shows that the hypothesis is a plausible one; see also [3]. This is shown in figure 4.
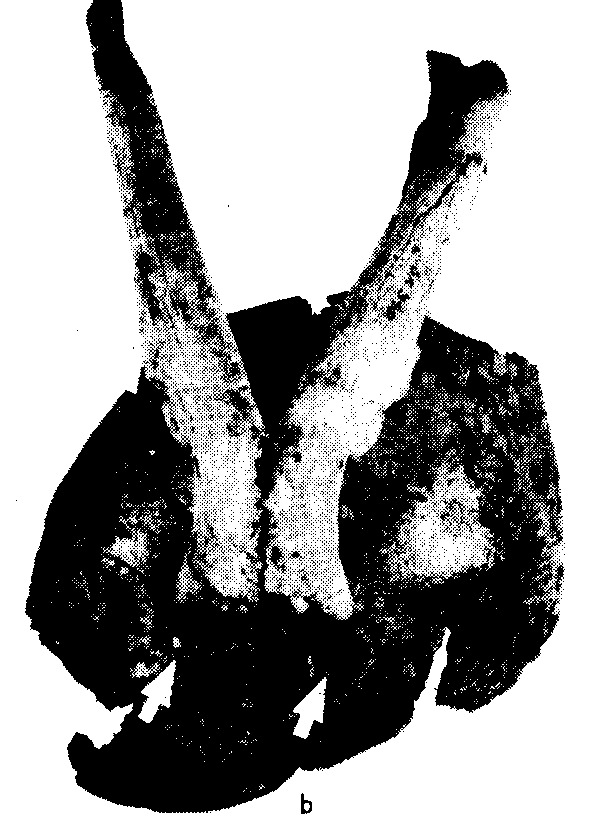
Figure 4. Fossil leopard jaw SK349 fitted into the notches of SK54 [2, p. 1117]
This explanation of the notches in SK54 also accords with several other facts about the debris in the Swartkrans cave. The entrance to the cave was a vertical shaft when the australopithecine remains were deposited and those remains are mostly comprised of skull fragments. Similar shaft caves in the area today are frequented by leopards which use the trees which grow around the entrances as places to safely consume prey out of the reach of hyenas. Since leopards tend to destroy the skeletal material of their primate prey with the exception of the skulls, the leopard-predator hypothesis would also explain why the australopithecine remains are mostly skull fragments---the skulls would simply have fallen from the trees and into the cave shafts [2]. This scenario, leopard predation of early hominids, is much different from the ``killer ape'' scenario favored by Dart.
Brain's leopard hypothesis exemplifies the use of visual abduction. The target of explanation---the unusual notches in the skullcap SK54---are highly visual in nature, consisting in their placement, depth, and direction. The hypothesis reconstructs the vital moment in the history of an unfortunate hominid, when its head was clenched in the jaws of a leopard to produce the notches. Because the relevant data are spatial, the hypothesis is most parsimoniously captured visually, as in figure 3, and may well have first occurred to Brain as just such a mental picture. The hypothesis thus abduced was then corroborated by further evidence of fossil leopard jaws and the feeding habits of modern leopards. Thus, this example illustrates that visual abduction fits the expanded criteria for abduction discussed in section 2.
Abduction is often thought of as a kind of reverse deduction; see section 2.1. Whereas modus ponens infers from p right arrow q and p to q, abduction infers from p right arrow q and q to p. This formulation trivializes the point of abduction, which is to form and evaluate hypotheses that make sense of puzzling facts. Making sense is a holistic matter of fitting the puzzling facts into a coherent pattern of representations. The notion of coherence has usually remained vague, but Thagard and Verbeurgt [29] have recently defined coherence in terms of maximization of constraint satisfaction. After briefly stating their definition, we will show how abduction can be reconceptualized as a coherence problem.
Let E be a finite set of elements ei and C be a set of constraints on E understood as a set (ei, ej) of pairs of elements of E. C divides into C+, the positive constraints on E, and C-, the negative constraints on E. With each constraint is associated a number w, which is the weight (strength) of the constraint. The problem is to partition E into two sets, A (accepted) and R (rejected), in a way that maximizes compliance with the following two coherence conditions:
1. if (ei, ej) is in C+, then ei is in A if and only if ej is in A;
2. if (ei, ej) is in C-, then ei is in A if and only if ej is in R.
Let W be the weight of the partition, that is, the sum of the weights of the satisfied constraints. The coherence problem is then to partition E into A and R in a way that maximizes W.
To understand abduction as a coherence problem, we need to specify the elements and the constraints. The elements are representations of causes and effects; in line with our discussion of visual abduction, we will allow the representations to include both sentential and nonsentential representations such as visual ones. The major positive constraint on abduction is that if one element explains another, then there is a symmetric positive constraint between them. In accord with the first of the two coherence constraints above, this will have the effect that if the explaining element and the explained element will tend to be accepted or rejected together. If, as often happens, more than one element is required to explain another element, the weight on the constraint between each explaining element and the explained element can be less than if there were only one explaining element, in keeping with the theory of simplicity of Thagard [28].
Two sorts of negative constraint are possible. If two elements contradict each other, then there is a symmetric negative constraint between them, but there is also a negative constraint if two elements offer competing explanations of the same fact [28]. Deciding which explanatory hypotheses to accept and which to reject is a matter of maximizing compliance with the two coherence conditions. Computationally, this is a very difficult problem and no tractable algorithm for solving it is available, although various approximation algorithms work quite well [29].
Our account of abduction as a coherence problem avoids all the limitations we discussed in section 2. We assume that the relation between elements is explanation, not deduction. Elements can explain other elements which explain other elements, so hypotheses can be layered and give rise to complex chains of constraints. Abduction is not defined in terms of a fixed set of elements but allows the possibility of creation of new elements that produce a new assessment of coherence. New hypotheses need not be consistent with existing ones, nor need the facts be completely explained. Maximizing coherence involves explaining as much as possible (positive constraints) and being as consistent as possible (negative constraints), but perfection is not to be sought in abductive reasoning. We are not urging inconsistency as a general epistemological strategy, only noting that it is sometimes necessary to form hypotheses inconsistent with what is currently accepted in order to provoke a general belief revision that can restore consistency.
Reducing the weights on constraints when explanation is accomplished by multiple hypotheses allows a complex assessment of simplicity. Finally, since elements can be visual or other nonverbal kinds of representation, we have transcended the limitation of abductive reasoning to sentences.
The definitions of abduction proposed by Konolige and by Bylander, Allemang, Tanner and Josephson are clearly inadequate as general characterizations of this important type of reasoning. These definitions made possible precise comparisons with other models and derivation of complexity theoretic results, but the results must be viewed as relative to the abstract model of abduction proposed. One might think that all complexity results would carry over to models of abduction more elaborate than the ones offered: if abduction is more complicated than Bylander et al. allow, then the computational complexity should be at least as great, so abduction would still be NP-hard. But the main results of Bylander et al. concern the difficulty of determining whether an explanation exists, where their notion of explanation is, as we saw, unrealistically restricted to cases where all the data are to be explained. In scientific reasoning, in contrast, the task is to explain as much of the data as you can and to come up with a set of explanatory hypotheses that is better than the current set. It is a matter of satisficing (choosing the most coherence set of hypotheses) rather than optimizing. Abduction characterized in terms of coherence is still intractable, but efficient approximation algorithms exist. There is also the possibility that heuristic search made possible by visual representations can greatly improve the computability of abductions, although this remains to be shown.
Thanks to important formal results such as the theory of NP-completeness, formal methods have achieved much well-deserved prestige in computer science and artificial intelligence. But an oversimplified formalization can distract from important aspects of the kinds of reasoning that underlie intelligence. Graph grammars and other techniques for visual representation offer the prospects of developing more general accounts of the nature of abductive reasoning, which should be construed not as a deviant form of deduction, but as a coherence problem.
* We are grateful to John Josephson and Don Roberts for comments on an earlier draft. Thanks to John Ching and Andrew Wong for ideas about graphical representations. This research was supported by the National Science and Engineering Research Council of Canada.
[1] R. Ardrey. African genesis: A personal investigation into the animal origins and nature of man. Atheneum, Ney York, N.Y., 1961.
[2] C. K. Brain. New finds at the Swartkrans australopithecine site. Nature, 225:1112-9, 1970.
[3] C. K. Brain. The hunters or the hunted? An introduction to African cave taphonomy. The University of Chicago Press, Chicago, Ill., 1981.
[4] T. Bylander, D. Allemang, M.C. Tanner, and J.R. Josephson. The computational complexity of abduction. Artificial Intelligence, 49:25-60.
[5] J. Y. Ching. Computational imagery: An alternative framework. Ph.D. thesis proposal, Pattern Analysis and Machine Intelligence Lab, University of Waterloo, Waterloo, On., May 1994.
[6] R. A. Dart. The predatory transition from ape to man. International Anthropological Linguistic Review, 1(4):201-18, 1953.
[7] H. Ehrig, H. J. Kreowski, and G. Rozenberg, editors. Graph-grammars and their application to computer science:4th international workshop, number 532 in Lecture notes in computer science, Berlin, Germany, March 1990. European Association for theoretical computer science, Springer Verlag.
[8] J. I. Glasgow. The imagery debate revisited: A computational perspective. Computational Intelligence, 9:309-33, 1993.
[9] J. I. Glasgow and D. Papadias. Computational imagery. Cognitive Science, 17930:355-394, 1992.
[10] T. A. Goudge. The thought of C. S. Peirce. University of Toronto Press, Toronto, On., Canada, 1950.
[11] C. Hartshorne and P. Weiss, editors. Collected papers of Charles Sanders Peirce. Harvard University Press, Cambridge, Mass., U.S.A., 1958. Volumes 7-8 edited by A. Burks.
[12] C. G. Hempel. Aspects of scientific explanation. The Free Press, New York, N.Y., 1965.
[13] J.R. Hobbs, M. Stickel, D. Appelt, and P. Martin. Interpretation as abduction. Technical Note 499, AI Center, SRI International, 333 Ravenswood Ave., Menlo Park, CA 94025, December 1990.
[14] C.V. Jones. An integrated modeling environment base on attributed graphs and graph-grammars. Decision Support Systems: The international journal, 9(10):255-72, 1991.
[15] P. Kitcher and W. Salmon. Scientific explanation. University of Minnesota Press, Minneapolis, M.N., 1989.
[16] K. Konolige. Abduction versus closure in causal theories. Artificial Intelligence, 52:255-72, 1991.
[17] M. Leyton. Inferring causal history from shape. Cognitive Science, 13:357-87, 1989.
[18] D. V. McDermott. A critique of pure reason. Computational Intelligence, 3:151-60,1987.
[19] M. Nagl. Formal languages of labelled graphs. Computing, 16:113-37, 1976.
[20] J. Pearl. Probabilistic reasoning in intelligent systems. Morgan Kaufman, San Mateo, CA, 1988.
[21] Y. Peng and J. Reggia. Abductive inference models for diagnostic problem solving. Springer Verlag, New York, N.Y., 1990.
[22] R. Reiter. A theory of diagnosis from first principles. Artificial Intelligence, 32:57-95, 1987.
[23] D. D. Roberts. The existential graphs of Charles S. Peirce. Mouton, The Hague, 1973.
[24] C. Shelley. Visual abductive reasoning in archaeology. Under review, 1996.
[25] P. Thagard. Computational philosophy of science. MIT Press, Cambridge, Mass., 1988.
[26] P. Thagard. Explanatory coherence. Behavioral and Brain Sciences, 12:435-67, 1989.
[27] P. Thagard. Philosophical and computational models of explanation. Philosophical Studies, 64:87-104, 1991.
[28] P. Thagard. Conceptual revolutions. Princeton University Press, Princeton, N.J., 1992.
[29] P. Thagard and K. Verbeurgt. Coherence. Under review.
[30] A. Wong, S. Lu, and M. Rioux. Recognition and shape synthesis of 3-D objects based on attributed hypergraphs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(3):279-90, Jun 1989.