Philosophy Department
University of Waterloo
Waterloo, Ontario, N2L 3G1
pthagard@watarts.uwaterloo.ca
© Paul Thagard and Karsten Verbeurgt, 1997
To go directly a particular section of this paper, click on a section title below.
| 1 Introduction |
| 2 Coherence as Constraint Satisfaction |
| 3 Coherence Problems |
| 4 Computing Coherence |
| 5 Measuring Coherence |
| 6 Circularity and Truth |
| 7 Conclusion |
To return to the Coherence Articles Table of Contents page, click here.
Abstract
This paper provides a computational characterization of coherence that applies to a wide range of philosophical problems and psychological phenomena. Maximizing coherence is a matter of maximizing satisfaction of a set of positive and negative constraints. After comparing five algorithms for maximizing coherence, we show how our characterization of coherence overcomes traditional philosophical objections about circularity and truth.
The concept of coherence has been important in many areas of philosophy and psychology. In metaphysics, there have been advocates of a coherence theory of truth. More commonly, in epistemology there have been advocates of coherence theories of epistemic justification, some of them emphasizing explanatory coherence. In logic, some theorists have contended that principles of reasoning are to be defended not on the basis of their a priori validity but on the basis of their coherence with inferential practice. Similarly, some ethical theorists have sought to defend general ethical principles on the basis of their coherence with particular ethical judgments, where coherence is judged through a process of achieving reflective equilibrium. Psychologists have also employed the concept of coherence to help understand processes as diverse as word perception, discourse comprehension, analogical mapping, cognitive dissonance, and interpersonal impression formation.
But what is coherence? Given a large number of elements (propositions, concepts, or whatever) that are coherent or incoherent with each other in various ways, how can we accept some of these elements and reject others in a way that maximizes coherence? How can coherence be computed?
Section 2 of this paper offers a simple characterization of coherence problems that is general enough to apply to a wide range of current philosophical and psychological applications summarized in section 3. Maximizing coherence is a matter of maximizing satisfaction of a set of positive and negative constraints. Section 4 describes five algorithms for computing coherence, including a connectionist method from which our characterization of coherence was abstracted. Coherence problems are inherently intractable computationally, in the sense that, under widely held assumptions of computational complexity theory, there are no efficient (polynomial-time) procedures for solving them. There exist, however, several effective approximation algorithms for maximizing coherence problems, including one using connectionist (neural network) techniques. Different algorithms yield different methods for measuring coherence discussed in section 5. We conclude by showing in section 6 that our methods of computing coherence overcome the traditional philosophical objection that coherence theories are circular and ineffective in achieving truth..
This paper is intended to make contributions to philosophy, psychology, and computer science. The notion of coherence has been widely used in philosophy, particularly in ethics and epistemology, but has been left completely vague. In contrast, we present a characterization of coherence which is as mathematically precise as the tools of deductive logic and probability theory more commonly used in philosophy. The psychological contribution of this paper is that it provides an abstract formal characterization that unifies numerous psychological theories. We provide a new mathematical framework that encompasses constraint satisfaction theories of hypothesis evaluation, analogical mapping, discourse comprehension, impression formation, and so on. Previously, these theories shared an informal characterization of cognition as parallel constraint satisfaction, along with use of connectionist algorithms to perform constraint satisfaction. Our new precise account of coherence makes clear what these theories have in common besides connectionist implementations. Moreover, our mathematical characterization generates results of considerable computational interest, including proof that the coherence problem is NP-hard and development of algorithms that provide non-connectionist means of computing coherence. Finally, in its display of interconnections among important problems in philosophy, psychology, and computer science, this paper illustrates the multidisciplinary nature of cognitive science.
When we make sense of a text, a picture, a person, or an event, we need to construct an interpretation that fits with the available information better than alternative interpretations. The best interpretation is one that provides the most coherent account of what we want to understand, considering both pieces of information that fit with each other and pieces of information that do not fit with each other. For example, when we meet unusual people, we may consider different combinations of concepts and hypotheses that fit together to make sense of their behavior.
Coherence can be understood in terms of maximal satisfaction of multiple constraints, in a manner informally summarized as follows:
1. Elements are representations such as concepts, propositions, parts of images, goals, actions, and so on.
2. Elements can cohere (fit together) or incohere (resist fitting together). Coherence relations include explanation, deduction, facilitation, association, and so on. Incoherence relations include inconsistency, incompatibility, and negative association.
3. If two elements cohere, there is a positive constraint between them. If two elements incohere, there is a negative constraint between them.
4. Elements are to be divided into ones that are accepted and ones that are rejected.
5. A positive constraint between two elements can be satisfied either by accepting both of the elements or by rejecting both of the elements.
6. A negative constraint between two elements can be satisfied only by accepting one element and rejecting the other.
7. The coherence problem consists of dividing a set of elements into accepted and rejected sets in a way that satisfies the most constraints.
Examples of coherence problems are given in section 2.
More precisely, consider a set E of elements which may be propositions or other representations. Two members of E, e1 and e2, may cohere with each other because of some relation between them, or they may resist cohering with each other because of some other relation. We need to understand how to make E into as coherent a whole as possible by taking into account the coherence and incoherence relations that hold between pairs of members of E. To do this, we can partition E into two disjoint subsets, A and R, where A contains the accepted elements of E, and R contains the rejected elements of E. We want to perform this partition in a way that takes into account the local coherence and incoherence relations. For example, if E is a set of propositions and e1 explains e2, we want to ensure that if e1 is accepted into A then so is e2. On the other hand, if e1 is inconsistent with e3, we want to ensure that if e1 is accepted into A, then e3 is rejected into R. The relations of explanation and inconsistency provide constraints on how we decide what can be accepted and rejected.
More formally, we can define a coherence problem as follows. Let E be a finite set of elements {ei} and C be a set of constraints on E understood as a set {(ei, ej)} of pairs of elements of E. C divides into C+, the positive constraints on E, and C-, the negative constraints on E. With each constraint is associated a number w, which is the weight (strength) of the constraint. The problem is to partition E into two sets, A and R, in a way that maximizes compliance with the following two coherence conditions:
1. if (ei, ej) is in C+, then ei is in A if and only if ej is in A.
2. if (ei, ej) is in C-, then ei is in A if and only if ej is in R.
Let W be the weight of the partition, that is, the sum of the weights of the satisfied constraints. The coherence problem is then to partition E into A and R in a way that maximizes W. (The appendix gives a graph theoretic definition of the coherence problem.) Because a coheres with b is a symmetric relation, the order of the elements in the constraints does not matter.
Intuitively, if two elements are positively constrained, we want them either to be both accepted or both rejected. On the other hand, if two elements are negatively constrained, we want one to be accepted and the other rejected. Note that these two conditions are intended as desirable results, not as strict requisites of coherence: the partition is intended to maximize compliance with them, not necessarily to ensure that all the constraints are simultaneously satisfied, since simultaneous satisfaction may be impossible. The partition is coherent to the extent that A includes elements that cohere with each other while excluding ones that do not cohere with those elements. We can define the coherence of a partition of E into A and R as W, the sum of the weights of the constraints on E that satisfy the above two conditions. Coherence is maximized if there is no other partition that has greater total weight.
This abstract characterization applies to the primary philosophical and psychological discussions of coherence. (1) To show that a given problem is a coherence problem in this sense, it is necessary to specify the elements and constraints, provide an interpretation of acceptance and rejection, and show that solutions to the given problem do in fact involve satisfaction of the specified constraints.
In coherence theories of truth, the elements are propositions, and accepted propositions are interpreted as true, while rejected propositions are interpreted as false. Advocates of coherence theories of truth have often been vague about the constraints, but entailment is one relation that furnishes a positive constraint and inconsistency is a relation that furnishes a negative constraint (Blanshard, 1939). Whereas coherence theories of justification interpret "accepted" as "judged to be true", coherence theories of truth interpret "accepted" as "true." (2)
Epistemic justification is naturally described as a coherence problem as specified above. Here the elements E are propositions, and the positive constraints can be a variety of relations among propositions, including entailment and also more complex relations such as explanation. (3) The negative constraints can include inconsistency, but also weaker constraints such as competition. Some propositions are to be accepted as justified, while others rejected. Thagard's (1989, 1992c) theory of explanatory coherence shows how constraints can be specified. In that theory, positive constraints arise from relations of explanation and analogy that hold between propositions, and negative constraints arise either because two hypotheses contradict each other or because they compete with each other to explain the same evidence.
Irvine has argued that the justification of mathematical axioms is similarly a matter of coherence (Irvine, 1994; see also Kitcher, 1983). Axioms are accepted not because they are a priori true, but because they serve to generate and systematize interesting theorems, which are themselves justified in part because they follow from the axioms. Goodman contended that the process of justification of logical rules is a matter of making mutual adjustments between rules and accepted inferences, bringing them into conformity with each other (Goodman, 1965; Thagard, 1988, ch. 7). Logical justification can then be seen as a coherence problem: the elements are logical rules and accepted inferences; the positive constraints derive from justification relations that hold between particular rules and accepted inferences; and the negative constraints arise because some rules and inferences are inconsistent with each other.
Similarly, Rawls (1971) argued that ethical principles can be revised and accepted on the basis of their fit with particular ethical judgments. Determining fit is achieved by adjusting principles and judgments until a balance between them, reflective equilibrium, is achieved. Daniels (1979) advocated that wide reflective equilibrium should also require taking into account relevant empirical background theories. Brink (1989) defended a theory of ethical justification based on coherence between moral theories and considered moral beliefs. Swanton (1992) proposed a coherence theory of freedom based on reflective equilibrium considerations. As in Goodman's view of logical justification, the acceptance of ethical principles and ethical judgments depends on their coherence with each other. Coherence theories of law have also been proposed, holding the law to be the set of principles that makes the most coherent sense of court decisions and legislative and regulatory acts (Raz, 1992).
Thagard and Millgram (1995; Millgram and Thagard, 1996) have argued that practical reasoning also involves coherence judgments about how to fit together various possible actions and goals. On their account, the elements are actions and goals, the positive constraints are based on facilitation relations (action A facilitates goal G), and the negative constraints are based on incompatibility relations (you cannot go to Paris and London at the same time). Deciding what to do is based on inference to the most coherent plan, where coherence involves evaluating goals as well as deciding what to do. Hurley (1989) has also advocated a coherence account of practical reasoning, as well as ethical and legal reasoning.
In psychology, various perceptual processes such as stereoscopic vision and interpreting ambiguous figures are naturally interpreted in terms of coherence and constraint satisfaction (Marr and Poggio, 1976; Feldman, 1981). Here the elements are hypotheses about what is being seen, and positive constraints concern various ways in which images can be put together. Negative constraints concern incompatible ways of combining images, for example seeing the same part of an object as both its front and its back. Word perception can be viewed as a coherence problem in which hypotheses about how letters form words can be evaluated against each other on the basis of constraints on the shapes and interrelations of letters (McClelland and Rumelhart, 1981). Kintsch (1988) described discourse comprehension as a problem of simultaneously assigning complementary meanings to different words in a way that forms a coherent whole. For example, the sentence "the pen is in the bank" can mean that the writing implement is in the financial institution, but in a different context it can mean that the animal containment is in the side of the river. In this coherence problem, the elements are different meanings of words and the positive constraints are given by meaning connections between words like "bank" and "river". Other discussions of natural language processing in terms of parallel constraint satisfaction include St. John and McClelland (1992) and MacDonald, Pearlmutter, and Seidenberg (1994). Analogical mapping can also be viewed as a coherence problem, in which two analogs are put into correspondence with each other on the basis of various constraints such as similarity, structure, and purpose (Holyoak and Thagard, 1989, 1995).
Coherence theories are also important in recent work in social psychology. Read and Marcus-Newhall (1993) have experimental results concerning interpersonal relations that they interpret in terms of explanatory coherence. Shultz and Lepper (1996) have reinterpreted old experiments about cognitive dissonance in terms of parallel constraint satisfaction. The elements in their coherence problem are beliefs and attitudes, and dissonance reduction is a matter of satisfying various positive and negative constraints. Kunda and Thagard (1996) have shown how impression formation, in which people make judgments about other people based on information about stereotypes, traits, and behaviors can also be viewed as a kind of coherence problem. The elements in impression formation are the various characteristics that can be applied to people; the positive constraints come from correlations among the characteristics; and the negative constraints come from negative correlations. For example, if you are told that someone is a Mafia nun, you have to reconcile the incompatible expectations that she is moral (nun) and immoral (Mafia).
Important political and economic problems can also be reconceived in terms of parallel constraint satisfaction. Arrow (1963) showed that standard assumptions used in economic models of social welfare are jointly inconsistent. Mackie (forthcoming) argues that deliberative democracy should not be thought of in terms of the idealization of complete consensus, but in terms of a group process of satisfying numerous positive and negative constraints. Details remain to be worked out, but democratic political decision appears to be a matter of both explanatory and deliberative coherence. Explanatory coherence is required for judgments of fact that are relevant to decisions, and multi-agent deliberative coherence is required for choosing what is optimal for the group as a whole.
Table 1 summarizes the various coherence problems that have been described in this section.
| Problem | Elements | Positive constraints | Negative constraints | Accepted as |
|---|---|---|---|---|
| Truth | propositions | entailment, etc. | inconsistency | true |
| Epistemic justification | propositions | entailment, explanation, etc. | inconsistency, competition | known |
| Mathematics | axioms, theorems | deduction | inconsistency | known |
| Logical justification | principles, practices | justify | inconsistency | justified |
| Ethical justification | principles, judgments | justify | inconsistency | justified |
| Legal justification | principles, court decisions | justify | inconsistency | justified |
| Practical reasoning | actions, goals | facilitation | incompatibility | desirable |
| Perception | images | connectedness, parts | inconsistency | seen |
| Discourse comprehension | meanings | semantic relatedness | inconsistency | understood |
| Analogy | mapping hypotheses | similarity, structure, purpose | 1-1 mappings | corresponding |
| Cognitive dissonance | beliefs, attitudes | consistency | inconsistency | believed |
| Impression formation | stereotypes, traits | association | negative association | believed |
| Democratic deliberation | actions, goals, propositions | facilitation, explanation | incompatible actions and beliefs | joint action |
Table 1. Kinds of coherence problem.
If coherence can indeed be generally characterized in terms of satisfaction of multiple positive and negative constraints, we can precisely address the question of how coherence can be computed, i.e. how elements can be selectively accepted or rejected in a way that maximizes compliance with the two coherence conditions on constraint satisfaction. This section describes five algorithms for maximizing coherence:
1. an exhaustive search algorithm that considers all possible solutions;
2. an incremental algorithm that considers elements in arbitrary order;
3. a connectionist algorithm that uses an artificial neural network to assess coherence;
4. a greedy algorithm that uses locally optimal choices to approximate a globally optimal solution;
5. a semidefinite programming (SDP) algorithm that is guaranteed to satisfy a high proportion of the maximum satisfiable constraints.
The first two algorithms are of limited use, but the others provide effective means of computing coherence.
The obvious way to maximize coherence is to consider all the different ways of accepting and rejecting elements. Here is the exhaustive algorithm:
1. Generate all possible ways of dividing elements into accepted and rejected.
2. Evaluate each of these for the extent to which it achieves coherence.
3. Pick the one with highest value of W.
The problem with this approach is that for n elements, there are 2n possible acceptance sets. A small coherence problem involving only 100 propositions would require considering 2 E100 =1,267,650,600,228,229,401,496,703,205,376 different solutions. No computer, and presumably no mind, can be expected to compute coherence in this way except for trivially small cases.
In computer science, a problem is said to be intractable if there is no polynomial-time solution to it, i.e. if the amount of time required to solve it increases at a faster-than-polynomial rate as the problem grows in size. For intractable problems, the amount of time and memory space required to solve the problem increases rapidly as the problem size grows. Consider, for example, the problem of using a truth table to check whether a compound proposition is consistent. A proposition with n connectives requires a truth table with 2n rows. If n is small, there is no difficulty, but an exponentially increasing number of rows is required as n gets larger. Problems in the class NP include ones that can be solved in polynomial time by a nondeterministic algorithm that allows guessing.
Members of an important class of problems called NP-complete are equivalent to each other in the sense that if one of them has a polynomial time solution, then so do all the others. A new problem can be shown to be NP-complete by showing (a) that it can be solved in polynomial time by a nondeterministic algorithm, and (b) that a problem already known to be NP-complete can be transformed to it, so that a polynomial-time solution to the new problem would serve to generate a polynomial-time solution to all the other problems. If only (b) is satisfied, then the problem is said to be NP-hard, i.e. at least as hard as the NP-complete problems. In the past two decades, many problems have been shown to be NP-complete, and polynomial-time solutions have been found for none of them, so it is widely believed that the NP-complete problems are inherently intractable.
Millgram (1991) noticed that the problem of computing coherence appears similar to other problems known to be intractable and conjectured that the coherence problem is also intractable. He was right: In the appendix we show that MAX CUT, a problem in graph theory known to be NP-complete, can be transformed to the coherence problem. If there were a polynomial-time solution to coherence maximization, there would also be a polynomial-time solution to MAX CUT and all the other NP-complete problems. So, on the widely held assumption that P not= NP (i.e. that the class of problems solvable in polynomial time is not equal to NP), we can conclude that the general problem of computing coherence is computationally intractable. As the number of elements increases, a general solution to the problem of maximizing coherence will presumably require an exponentially increasing amount of time.
For epistemic coherence and any other kind that involves large numbers of elements, this result is potentially disturbing. Each person has thousands or millions of beliefs. Epistemic coherentism requires that justified beliefs must be shown to be coherent with other beliefs. But the transformation of MAX CUT to the coherence problem shows, assuming that P not= NP, that computing coherence will be an exponentially-increasing function of the number of beliefs.
Here is a simple, efficient serial algorithm for computing coherence:
1. Take an arbitrary ordering of the elements e1, ...en of E.
2. Let A and R, the accepted and rejected elements, be empty.
3. For each element ei in the ordering,
if adding ei to A increases the total weight of satisfied constraints more than adding it to R, then add ei to A;
otherwise, add ei to R.
The problem with this algorithm is that it is seriously dependent on the ordering of the elements. Suppose we have just 4 elements, such that there is a negative constraint between e1 and e2, and positive constraints between e1 and e3, e1 and e4, and e2 and e4. In terms of explanatory coherence, e1 and e2 could be thought of as competing hypotheses, with e1 explaining more than e2, as shown in figure 2. The three other algorithms for computing coherence discussed in this section accept e1, e3, and e4, while rejecting e2. But the serial algorithm will accept e2 if it happens to come first in the ordering. In general, the serial algorithm does not do as well as the other algorithms at satisfying constraints and accepting the appropriate elements. (5)
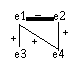
Figure 1. A simple coherence problem. Positive constraints are represented by thin lines, and the negative constraint is represented by a thick line.
Although the serial algorithm is not attractive prescriptively as an account of how coherence should be computed, it may well describe to some extent people's limited rationality. Ideally, a coherence inference should be nonmonotonic in that maximizing coherence can lead to rejecting elements that were previously accepted. In practice, however, limitations of attention and memory may lead people to adopt local, suboptimal methods for calculating coherence (Hoadley, Ranney, and Schank, 1994). Psychological experiments are needed to determine the extent to which people do coherence calculations suboptimally.
A more effective method for computing coherence uses connectionist (neural network) algorithms. This method is a generalization of methods that have been successfully applied in computational models of explanatory coherence, deliberative coherence, and elsewhere.
Here is how to translate a coherence problem into a problem that can be solved in a connectionist network:
1. For every element ei of E, construct a unit ui which is a node in a network of units . Such networks are very roughly analogous to networks of neurons .
2. For every positive constraint in C+ on elements ei and ej, construct a symmetric excitatory link between the corresponding units ui and uj.
3. For every negative constraint in C- on elements ei and ej, construct a symmetric inhibitory link between the corresponding units ui and uj.
4. Assign each unit ui an equal initial activation (say .01), then update the activation of all the units in parallel. The updated activation of a unit is calculated on the basis of its current activation, the weights on links to other units, and the activation of the units to which it is linked. A number of equations are available for specifying how this updating is done. (6) Typically, activation is constrained to remain between a minimum (e.g. -1) and a maximum (e.g. 1).
5. Continue the updating of activation until all units have settled - achieved unchanging activation values. If a unit ui has final activation above a specified threshold (e.g. 0), then the element ei represented by ui is deemed to be accepted. Otherwise, ei is rejected.
We thus get a partitioning of elements of E into accepted and rejected sets by virtue of the network U settling in such a way that some units are activated and others deactivated. Intuitively, this solution is a natural one for coherence problems. Just as we want two coherent elements to be accepted or rejected together, so two units connected by an excitatory link will tend to be activated or deactivated together. Just as we want two incoherent elements to be such that one is accepted and the other is rejected, so two units connected by an inhibitory link will tend to suppress each other's activation with one activated and the other deactivated. A solution that enforces the two conditions on maximizing coherence is provided by the parallel update algorithm that adjusts the activation of all units at once based on their links and previous activation values. Table 2 compares coherence problems and connectionist networks.
| Coherence | Connectionist network |
|---|---|
| element | unit |
| positive constraint | excitatory link |
| negative constraint | inhibitory link |
| conditions on coherence | parallel updating of activation |
| element accepted | unit activated |
| element rejected | unit deactivated |
Table 2. Comparison of coherence problems and connectionist networks.
Connectionist algorithms can be thought of as maximizing the "goodness-of-fit" or "harmony" of the network, defined by (Sigma)i(Sigma)jwijai(t)aj(t), where wij is the weight on the link between two units, and ai is the activation of a unit (Rumelhart, Smolensky, Hinton, and McClelland, 1986, p. 13). The characterization of coherence given in section 1 is an abstraction from the notion of goodness-of-fit. The value of this abstraction is that it provides a general account of coherence independent of neural network implementations and makes possible investigation of alternative algorithmic solutions to coherence problems. See section 5 for discussion of various measures of coherence.
Despite the natural fit between coherence problems and connectionist networks, the connectionist algorithms do not provide a universal, guaranteed way of maximizing coherence. We cannot prove in general that connectionist updating maximizes the two conditions on satisfying positive and negative constraints, since settling may achieve only a local maximum. Moreover, there is no guarantee that a given network will settle at all, let alone that it will settle in a number of cycles that is a polynomial function of the number of units.
While synchronous update networks, such as those used in this paper, are not generally guaranteed to converge, some convergence results are known for restricted network topologies. For example, Rodenhausen (1992) has shown that the neural networks used by Kintsch in his work on discourse comprehension will converge to a stable state if all connection weights are strictly positive, and if for every node in the network, the sum of the edge weights connected to that node is one. This result does not apply in general for the coherence networks discussed in this paper, because our networks include negative weights.
Other notable models in which convergence results can be shown are the models based on Ising spin glasses from statistical physics, such as Hopfield networks and Boltzmann machines. Hopfield (1982) showed that in a network with symmetrical connections, if node updates are asynchronous, then the network will converge to a local optimum. To overcome the problem of converging to a locally optimal state, the Boltzmann machine of Hinton and Sejnowski (1996) uses a simulated annealing technique to escape local minima. The simulated annealing technique, due to Kirkpatrick, Gelatt and Vecchi (1983), uses local gradient descent but allows for a jump to a lower energy state with a probability determined by the "temperature" of the system and the energy of that state. Both Hopfield Networks and the simulated annealing techniques used in Boltzmann machines have been used to approximate hard combinatorial problems, such as the traveling salesman problem (Hopfield and Tank, 1985; Kirkpatrick et. al. 1983). Obtaining the optimal ground state of any Ising spin glass model is shown by Barahona to solve the Max Cut problem (Barahona, 1982, Barahona and Titan, 1993). Thus, any algorithm guaranteed to achieve the optimal state would solve an NP-complete problem, so it is unlikely that any such algorithm exists.
While there are no mathematical guarantees on the quality of solutions produced by neural networks, empirical results for numerous connectionist models of coherence yield excellent results. ECHO is a computational model of explanatory coherence that has been applied to more than a dozen cases from the history of science and legal reasoning, including cases with more than 150 propositions. (Thagard, 1989, 1991, 1992a, 1992c; Nowak and Thagard, 1992a, 1992b; Eliasmith and Thagard, in press). (7) Computational experiments revealed that the number of cycles of activation updating required for settling does not increase as networks become larger: fewer than 200 cycles suffice for all ECHO networks tried so far. ARCS is a computational model of analog retrieval that selects a stored analog from memory on the basis of its having the most coherent match with a given analog (Thagard, Holyoak, Nelson, and Gochfeld, 1990). ARCS networks tend to be much larger than ECHO networks - up to more than 400 units and more than 10,000 links - but they still settle in fewer than 200 cycles, and the number of cycles for settling barely increases with network size. Thus quantitatively these networks are very well behaved, and they also produce the results that one would expect based on coherence maximization. For example, when ARCS is used to retrieve an analog for a representation of West Side Story from a data base of representations of 25 of Shakespeare's plays, it retrieves Romeo and Juliet.
The dozen coherence problems summarized in table 1 might give the impression that the different kinds of inference involved in all the problems occur in isolation from each other. But any general theory of coherence must be able to say how different kinds of coherence can interact. For example, the problem of other minds can be understood as involving both explanatory coherence and analogical coherence: the plausibility of my hypothesis that you have a mind is based both on it being the best explanation of your behavior and on the analogy between your behavior and my behavior (Holyoak and Thagard, 1995, ch. 7). The interconnections between different kinds of coherence can be modelled effectively by introducing new kinds of constraints between the elements of the different coherence problems. In the problem of other minds, the explanatory coherence element representing the hypothesis that you have a mind can be connected by a positive constraint with the analogical coherence element representing the mapping hypothesis that you are similar to me. Choosing the best explanation and the best analogy can then occur simultaneously as interconnected coherence processes. Similarly, ethical justification and epistemic justification can be intertwined through constraints that connect ethical principles and empirical beliefs, for example about human nature. A full, applied coherence theory would specify the kinds of connecting constraints that interrelate the different kinds of coherence problems. The parallel connectionist algorithm for maximizing coherence has no difficulty in performing the simultaneous evaluation of interconnected coherence problems.
Other algorithms are also available for solving coherence problems efficiently. We owe to Toby Donaldson an algorithm that starts with a randomly generated solution and then improves it by repeatedly flipping elements from the accepted set to the rejected set or vice versa. In computer science, a greedy algorithm is one that solves an optimization problem by making a locally optimal choice intended to lead to a globally optimal solution. Selman, Levesque, and Mitchell (1992) presented a greedy algorithm for solving satisfiability problems, and a similar technique produces the following coherence algorithm:
1. Randomly assign the elements of E into A or R.
2. For each element e in E, calculate the gain (or loss) in the weight of satisfied constraints that would result from flipping e, i.e. moving it from A to R if it is in A, or moving it from R to A otherwise.
3. Produce a new solution by flipping the element that most increases coherence, i.e. move it from A to R or from R to A. In case of ties, choose randomly.
4. Repeat 2 and 3 until either a maximum number of tries have taken place or until there is no flip that increases coherence.
On the examples on which we have tested it, this algorithm produces the same result as the connectionist algorithm, except that the greedy algorithm breaks ties randomly. (8) With its use of random solutions and a great many coherence calculations, this algorithm seems less psychologically plausible than the connectionist algorithm.
The proof in the appendix that the graph theory problem MAX CUT can be transformed to the coherence problem shows a close relation between them. MAX CUT is a difficult problem in graph theory that until recently had no good approximation: for twenty years the only available approximation technique known was one similar to the incremental algorithm for coherence we described above. This technique only guarantees an expected value of .5 times the optimal value. Recently, however, Goemans and Williamson (1994) discovered an approximation algorithm for MAX CUT that delivers an expected value of at least .87856 times the optimal value. Their algorithm depends on rounding a solution to a relaxation of a nonlinear optimization problem, which can be formulated as a semidefinite programming (SDP) problem, a generalization of linear programming to semidefinite matrices. Mathematical details are provided in the appendix.
What is important from the perspective of coherence are two results, one theoretical and the other experimental. Theoretically, the appendix proves that the semidefinite programming technique that was applied to MAX CUT can also be used for the coherence problem, with the same .878 performance guarantee: using this technique guarantees that the weight of the constraints satisfied by a partition into accepted and rejected will be at least .878 of the optimal weight. But where does this leave the connectionist algorithm which has no similar performance guarantee? We have run computational experiments to compare the results of the SDP algorithm to those produced by the connectionist algorithms used in existing programs for explanatory and deliberative coherence. (9) Like the greedy algorithm, the semidefinite programming solution handles ties between equally coherent partitions differently from the connectionist algorithm, but otherwise it yields equivalent results.
The formal constraint satisfaction characterization of coherence and the various algorithms for computing coherence suggest various means by which coherence can be measured. Such measurement is useful for both philosophical and psychological purposes. Philosophers concerned with normative judgments about the justification of belief systems naturally ask questions about the degree of coherence of a belief or set of beliefs. Psychologists can use degree of coherence as a variable to correlate with experimental measures of mental performance such as expressed confidence of judgments.
There are three sorts of measurement of coherence that are potentially useful:
1. the degree of coherence of an entire set of elements.
2. the degree of coherence of a subset of the elements.
3. the degree of coherence of a particular element.
The goodness-of-fit (harmony) measure of a neural network defined in section 4, (Sigma)i(Sigma)jwijai(t)aj(t), can be interpreted as the coherence of an entire set of elements that are assigned activation values that represent their acceptance and rejection. This measure is of limited use, however, since it is very sensitive to the number of elements, as well as to the particular equations used to update activation in the networks. Sensitivity to size of networks can be overcome by dividing goodness-of-fit by the number of elements or by the number of links or constraints (cf. Shultz and Lepper, 1996). Holyoak and Thagard (1989) found that goodness-of-fit did not give a reliable metric of the degree of difficulty of analogical mapping, which they instead measured in terms of the number of cycles required for a network to settle.
Network-independent measures of coherence can be stated in terms of the definition of a coherence problem given in section 2. For any partition of the set of elements into accepted and rejected, there is a measure W of the sum of the weights of the satisfied constraints. Let W_opt be the coherence of the optimal solution. The ideal measure of coherence achieved by a particular solution would be W/W_opt, the ratio of the coherence W of the solution to the coherence W_opt of the optimal solution; thus the best solution would have measure one. This measure is difficult to obtain, however, since the value of the optimal solution is not generally known. Another possible measure of coherence is the ratio W/W*, where W* is the sum of the weights of all constraints. This ratio does not necessarily indicate the closeness to the optimal solution as W/W_opt would, but it does have the property that the higher the ratio, the closer the solution is to optimal. Thus it gives a size-independent measure of coherence. In addition, when there is a solution where all constraints are satisfied, W/W* is equal to W/W_opt.
Neither goodness-of-fit nor W/W* provides a way of defining the degree of coherence of a subset of elements. This is unfortunate, since we would like be able to quantify judgments such as "Darwin's theory of evolution is more coherent than creationism.", where Darwin's theory consists of a number of hypotheses. The connectionist algorithm does provide a useful way to measure the degree of coherence of a particular element, since the activation of a unit represents the degree of acceptability of the element. Empirical tests of coherence theories have found strong correlations between experimental measurements of people's confidence about explanations and stereotypes and activation levels produced by connectionist models (Read and Marcus-Newhall, 1993; Kunda and Thagard, 1996; Schank and Ranney, 1992). The coherence of a set of elements can them be roughly measured as the mean activation of those elements. It would be desirable to define, within our abstract model of coherence as constraint satisfaction, a measure of the degree of coherence of a particular element or of a subset of elements, but it is hot clear how to do so. Such coherence is highly non-linear, since the coherence of an element depends on the coherence of all the elements that constrain it, including elements with which it competes. The coherence of a set of element is not simply the sum of the weights of the constraints satisfied by accepting them, but depends also on the comparative degree of constraint satisfaction of other elements that negatively constrain them.
Our characterization of coherence in terms of constraint satisfaction and our analysis of various algorithms for computing coherence are relevant to psychology, in that they provide a unified way of understanding diverse psychological phenomena (see Table 1). Our computational results are also of some psychological interest, particularly the finding that the coherence problem is NP-hard but nevertheless can be reliably approximated. Connectionist networks do not provide the only means of computing coherence, but they appear to work at least as well as less psychologically plausible computational techniques that have proven performance guarantees. Neural networks provide an efficient means for approximately solving the hard computational problem of computing coherence.
Our constraint-satisfaction characterization of coherence is particularly relevant to philosophy, where coherence ideas have been increasingly important for several decades, despite the lack of an exact notion of coherence. Compared to rigorous explorations of deductive logic and probability theory, coherence approaches to epistemology and ethics have been vague and imprecise. In contrast, we have presented a mathematically exact, computationally manageable, and psychologically plausible account of how coherence judgments can be made.
Our account of coherence provides an answer to some of the frequently offered objections to coherence theories in philosophy. In epistemology, foundationalists suppose that justification must be based on a set of elements that do not themselves need justification. Coherence theorists deny the existence of such given elements, and therefore must face the circularity objection. An element is accepted because it coheres with other elements which are themselves accepted because they cohere with other elements which are themselves ...., ad infinitum. From the perspective of formal logic, where premises justify their conclusions and not vice versa, coherentist justification seems viciously circular.
Coherentists such as Bosanquet (1920) and BonJour (1985) have protested that the circularity evident in coherence-based justification is not vicious, and the algorithms for computing coherence in section 4 show more precisely how a set of elements can depend on each other interactively. Using the connectionist algorithm, we can say that after a network of units has settled and some units are identified as being activated, then acceptance of each element represented by a unit is justified on the basis of its relation to all other elements. The algorithms for determining activation (acceptance) proceed fully in parallel, with each unit's activation depending on the activation of all connected units after the previous cycle. Because it is clear how the activation of each unit depends simultaneously on the activation of all other units, there need be no mystery about how acceptance can be the result of mutual dependencies. Similarly, the greedy and SDP algorithms in the appendix maximize constraint satisfaction globally, not by evaluating individual elements sequentially. Thus modern models of computation vindicate Bosanquet's claim that inference need not be interpreted within the confines of linear systems of logical inference.
Coherence-based inference involves no regress because it does not proceed in steps, but rather by simultaneous evaluation of multiple elements. Figure 2a shows a pattern of inference that would indeed be circular, but figure 2b shows the situation when a connectionist algorithm computes everything at once. Unlike entailment or conditional probability, coherence constraints are symmetric relations, making possible the double-headed arrows in figure 2b.
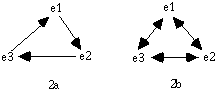
Figure 2. Circular versus non-circular justification.
Coherence-based reasoning is thus not circular, but it is still legitimate to ask whether it is effective. Do inferences based on explanatory and other kinds of coherence produce true conclusions? Early proponents of coherence theories of inference such as Blanshard (1939) also advocated a coherence theory of truth, according to which the truth of a proposition is constituted by its being part of a general coherent set of propositions. From the perspective of a coherence theory of truth, it is trivial to say that coherence-based inference produces truth (i.e. coherent) conclusions. But a major problem arises for coherentist justification with respect to a correspondence theory of truth, according to which the truth of a proposition is constituted by its relation to an external, mind-independent world.
Proponents of coherence theories of truth reject the idea of such an independent world, but considerations of explanatory coherence strongly support its existence. Why do different people have similar sensory experiences in similar situations? Why are scientists able to replicate each other experiments? Why are people unable to have just the sensory experiences they want? Why do scientists often get negative experimental results? Why does science often lead to technological successes? The best explanation of these phenomena is that there is an external world that operates independently of human minds and causally influences our perceptions and experimental results (see Thagard, 1988, ch. 8, for further argument). Hence truth is a matter of correspondence, not mere coherence.
Coherence theories of justification therefore have a serious problem in justifying the claim that they can lead to truth. Thagard, Elias, Rusnock, and Shelley (forthcoming) address this issue by distinguishing three kinds of coherence problems. A pure coherence problem is one that does not favor the acceptance of any particular set of elements. A foundational coherence problem selects a set of favored elements for acceptance as self-justified. A discriminating coherence problem favors a set of elements but their acceptance still depends on their coherence with all the other elements. The issue of correspondence is most acute for pure coherence problems, in which acceptance of elements is based only on their relation to each other. But the coherence theories that have so far been implemented computationally all treat coherence problems as discriminating. For example, explanatory coherence theory gives priority (but not guaranteed acceptance) to elements representing the results of observation and experiment (Thagard, 1992). Connectionist algorithms naturally implement this discrimination by spreading activation first to elements that should be favored in the coherence calculation. Then, assuming with the correspondence theory of truth that observation and experiment involve in part causal interaction with the world, we can have some confidence that the hypotheses adopted on the basis of explanatory coherence also correspond to the world and are not mere mind-contrivances that are only internally coherent.
The problem of correspondence to the world is even more serious for ethical justification, for it is not obvious how to legitimate a coherence-based ethical judgment such as "it is permissible to eat some animals but not people". Thagard (forthcoming) argues that ethical coherence involves complex interactions of deliberative, deductive, analogical, and explanatory coherence. In some cases the relative objectivity of explanatory coherence, discriminating as it does in favor of observation and experiment, can carry over to the objectivity of ethical judgments that also involve other kinds of coherence.
We have given a general characterization of coherence that applies to many areas of philosophy and psychology. The characterization is precise enough that its computational properties can be analyzed and general methods of computing coherence can be provided. Assessment of coherence can be done in ways that are computationally efficient, psychologically plausible, and philosophically acceptable in that they answer important objections that have been made against coherence theories. In the past, coherence views of inference have appeared vague in comparison to more rigorous views based on deductive logic and the probability calculus. But coherence theories can now be more fully specified by characterizing coherence as constraint satisfaction and by computing it using connectionist and other algorithms.
APPENDIX omitted
* We are grateful to Elijah Millgram for many excellent suggestions, to Chris Eliasmith for programming the SDP algorithm, and to them, Allison Barnes, Walter Kintsch, Michael Ranney, Miriam Solomon, and Cameron Shelley for comments on earlier drafts. This research is supported by the Natural Sciences and Engineering Research Council of Canada. Please send correspondence to Paul Thagard, Philosophy Department, University of Waterloo, Waterloo, Ontario, N2L 3G1, pthagard@watarts.uwaterloo.ca.
(1) Our characterization of coherence will not handle non-pairwise inconsistencies or incompatibilities, for example when three or more propositions are jointly inconsistent. Computationally, constraints that involve more than two elements are very difficult. An unrelated notion of coherence is used in probabilistic accounts of belief, where degrees of belief in a set of propositions are called coherent if they satisfy the axioms of probability. See Thagard (in press) for discussion of the relations between probability and explanatory coherence.
Many problems in artificial intelligence have been discussed in terms of constraint satisfaction. In AI terminology, the coherence problem is a partial constraint satisfaction problem. See Tsang (1993) and Freuder and Mackworth (1994).
(2) A coherence theory of truth may require that our second coherence condition be made more rigid, since two inconsistent propositions can never both be true. See section 6 for further discussion of truth.
(3) On epistemic coherence see: Audi (1993), Bender (1989), BonJour (1985). Davidson,(1986), Haack (1993), Harman (1973, 1986), Lehrer (1974, 1990), Rescher (1992).
(4) For a review of NP-completeness, see Garey and Johnson (1979). For an account of why computer scientists believe that PNP, see Thagard (1993).
(5) Rescher (1973) describes a complex serial procedure for deriving coherent truths from maximally consistent sets of data.
(6) See McClelland and Rumelhart (1989). For example, on each cycle the activation of a unit j , aj, can be updated according to the following equation:
{ netj(max- aj(t)) if netj > 0
aj(t+1) = aj(t)(1-d) +
{ netj(aj(t) - min) otherwise
Here d is a decay parameter (say .05) that decrements each unit at every cycle, min is a minimum activation (-1), max is maximum activation (1). Based on the weight wij between each unit i and j, we can calculate netj , the net input to a unit, by:
netj = (Sigma)iwijai(t).
(7) Glymour (1992) suggested that ECHO's calculation of explanatory coherence could be replaced by a few simple equations. Thagard (1992b) showed that his proposal produced unacceptable results (e.g. accepting some propositions of Ptolemaic astronomy over Copernican). The results reported in this section show why a simple solution to coherence calculations is unlikely to be found: the coherence problem is NP-hard, and approximation requires either connectionist algorithms such as those used in ECHO or nonlinear programming techniques of comparable power.
(8) Although the greedy algorithm largely replicates the performance of ECHO and DECO on the examples on which we have tried it, it does not replicate the performance of ACME which does analogical mapping not simply by accepting and rejecting hypotheses that represent the best mappings, but by choosing as best mappings hypotheses represented by units with higher activations that alternative hypotheses.
(9) Chris Eliasmith adapted a semidefinite programming solution to MAX
CUT to provide a similar solution to coherence problems, using MATLAB code
for MAX CUT given in Helmberg et al. (1996). LISP code for the exhaustive,
incremental, and connectionist algorithms, as well as MATLAB code for the
semidefinite programming algorithm, is available from Thagard.
Alizadeh, F. (1992). Combinatorial optimization with semi-definite matrices. In Proceedings of the 2nd conference on integer programming and combinatorial optimization (pp. 385-405). Pittsburgh: Carnegie Mellon University.
Arrow, K. J. (1963). Social choice and individual values (second ed.). New York: Wiley.
Audi, R. (1993). Fallibilist foundationalism and holistic coherentism. In L. P. Pojman (Eds.), The theory of knowledge: Classic and contemporary readings (pp. 263-279). Belmont, CA: Wadsworth.
Barahona, F. (1982). On the computational complexity of Ising spin glass models. Journal of Physics A: Mathematical and General, 15, 3241-3253.
Barahona, F., & Titan, H. (1993). Ground state magnetizations of the Ising model for spin glasses. Technical report CS-93-08, University of Waterloo Department of Computer Science. .
Bender, J. W. (Ed.). (1989). The current state of the coherence theory. Dordrecht: Kluwer.
Blanshard, B. (1939). The nature of thought, vol. 2. London: George Allen & Unwin.
BonJour, L. (1985). The structure of empirical knowledge. Cambridge, MA: Harvard University Press.
Bosanquet, B. (1920). Implication and linear inference. London: Macmillan.
Brink, D. O. (1989). Moral realism and the foundations of ethics. Cambridge: Cambridge University Press.
Daniels, N. (1979). Wide reflective equilibrium and theory acceptance in ethics. Journal of Philosophy, 76, 256-282.
Davidson, D. (1986). A coherence theory of truth and knowledge. In E. Lepore (Eds.), Truth and interpretation Oxford: Basil Blackwell.
Davies, P., & Brown, J. (1988). Superstrings. Cambridge: Cambridge University Press.
Eliasmith, C., & Thagard, P. (in press). Waves, particles, and explanatory coherence. British Journal for the Philosophy of Science.
Feldman, J. A. (1981). A connectionist model of visual memory. In G. E. Hinton & J. A. Anderson (Eds.), Parallel models of associative memory (pp. 49-81). Hillsdale, NJ: Erlbaum.
Freuder, E. C., & Mackworth, A. K. (Ed.). (1994). Constraint based reasoning. Cambridge, MA: MIT Press.
Garey, M., & Johnson, D. (1979). Computers and intractability. New York: Freeman.
Glymour, C. (1992). Invasion of the mind snatchers. In R. N. Giere (Eds.), Cognitive Models of Science, Minnesota Studies in the Philosophy of Science, vol. 15 (pp. 465-471). Minneapolis: University of Minnesota Press.
Goemans, M. X., & Williamson, D. P. (1994). .878-Approximation algorithms for MAX CUT and MAX 2SAT. Proceedings of the 26 annual ACM STOC, Montreal, 422-431.
Goodman, N. (1965). Fact, fiction and forecast (2 ed.). Indianapolis: Bobbs-Merrill.
Haack, S. (1993). Evidence and inquiry: Towards reconstruction in epistemology. Oxford: Blackwell.
Harman, G. (1973). Thought. Princeton: Princeton University Press.
Harman, G. (1986). Change in view: Principles of reasoning. Cambridge, MA: MIT Press/Bradford Books.
Helmberg, C., Rendl, F., Vanderbei, R. J., & Wolkowicz, H. (1996). An interior-point method for semidefinite programming. SIOPT, 6, 342-361.
Hinton, G. E., & Sejnowski, T. J. (1986). Learning and relearning in Boltzmann machines. In D. E. Rumelhart & J. L. McCelland (Eds.), Parallel distributed processing: Explorations in the microstructure of cognition (pp. 282-317). Cambridge, MA: MIT Press.
Hoadley, C. M., Ranney, M., & Schank, P. (1994). WanderECHO: A connectionist simulation of limited coherence. In A. Ran & K. Eiselt (Eds.), Proceedings of the sixteenth annual conference of the cognitive science society (pp. 421-426). Hillsdale, NJ: Erlbaum.
Holyoak, K. J., & Thagard, P. (1989). Analogical mapping by constraint satisfaction. Cognitive Science, 13, 295-355.
Holyoak, K. J., & Thagard, P. (1995). Mental leaps: Analogy in creative thought. Cambridge, MA: MIT Press/Bradford Books.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences, 79, 2554-2558.
Hopfield, J. J., & Tank, D. W. (1985). Neural computation of decisions in optimization problems. Biological Cybernetics, 52, 141-152.
Hurley, S. L. (1989). Natural reasons: Personality and polity. New York: Oxford University Press.
Irvine, A. (1994). Experiments in mathematics, talk given at the University of Waterloo. .
Kintsch, W. (1988). The role of knowledge in discourse comprehension: A construction-integration model. Psychological Review, 95, 163-182.
Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220, 771-680.
Kitcher, P. (1983). The nature of mathematical knowledge. New York: Oxford University Press.
Kunda, Z., & Thagard, P. (1996). Forming impressions from stereotypes, traits, and behaviors: A parallel-constraint-satisfaction theory. Psychological Review, 103, 284-308.
Lehrer, K. (1974). Knowledge. Oxford: Clarendon Press.
Lehrer, K. (1990). Theory of knowledge. Boulder: Westview.
MacDonald, M. C., Pearlmutter, N. J., & Seidenberg, M. S. (1994). Lexical nature of syntactic ambiguity resolution. Psychological Review, 101, 676-703.
Mackie, G. (forthcoming). A parallel constraint satisfaction model of deliberative democracy. Manuscript in progress, Oxford University. .
Marr, D., & Poggio, T. (1976). Cooperative computation of stereo disparity. Science, 194, 283-287.
McClelland, J. L., & Rumelhart, D. E. (1981). An interactive activation model of context effects in letter perception: Part 1: An account of basic findings. Psychological Review, 88, 375-407.
McClelland, J. L., & Rumelhart, D. E. (1989). Explorations in parallel distributed processing. Cambridge, MA: MIT Press.
Millgram, E. (1991). Harman's hardness arguments. Pacific Philosophical Quarterly, 72, 181-202.
Millgram, E., & Thagard, P. (1996). Deliberative coherence. Synthese, 108, 63-88.
Nowak, G., & Thagard, P. (1992a). Copernicus, Ptolemy, and explanatory coherence. In R. Giere (Eds.), Cognitive models of science, (pp. 274-309). Minneapolis: University of Minnesota Press.
Nowak, G., & Thagard, P. (1992b). Newton, Descartes, and explanatory coherence. In R. Duschl & H. R. (Eds.), Philosophy of Science, Cognitive Psychology and Educational Theory and Practice. (pp. 69-115). Albany: SUNY Press.
Rawls, J. (1971). A theory of justice. Cambridge, MA: Harvard University Press.
Raz, J. (1992). The relevance of coherence. Boston University Law Review, 72, 273-321.
Read, S., & Marcus-Newhall, A. (1993). The role of explanatory coherence in the construction of social explanations. Journal of Personality and Social Psychology, 65, 429-447.
Rescher, N. (1973). The coherence theory of truth. Oxford: Clarendon Press.
Rescher, N. (1992). A system of pragmatic idealism, volume 1: Human knowledge in idealistic perspective. Princeton: Princeton University Press.
Rodenhausen, H. (1992). Mathematical aspects of Kintsch's model of discourse comprehension. Psychological Review, 99, 547-549.
Rumelhart, D., Smolensky, P., Hinton, G., & McClelland, J. (1986). Schemata and sequential thought processes in PDP models. In J. McClelland & D. Rumelhart (Eds.), Parallel distributed processing: Explorations in the microstructure of cognition (pp. 7-57). Cambridge MA: MIT Press/Bradford Books.
Schank, P., & Ranney, M. (1992). Assessing explanatory coherence: A new method for integrating verbal data with models of on-line belief revision. In Proceedings of the Fourteenth Annual Conference of the Cognitive Science Society (pp. 599-604). Hillsdale, NJ: Erlbaum.
Selman, B., Levesque, H., & Mitchell, D. (1992). A new method for solving hard satisfiability problems. In Proceedings of the tenth national conference on artificial intelligence (pp. 440-446). Menlo Park: AAAI Press.
Shultz, T. R., & Lepper, M. R. (1992). A constraint satisfaction model of cognitive dissonance phenomena. In Proceedings of the Fourteenth Annual Conference of the Cognitive Science Society (pp. 462-467). Hillsdale, NJ:: Erlbaum.
St. John, M. F., & McClelland, J. L. (1992). Parallel constraint satisfaction as a comprehension mechanism. In R. G. Reilly & N. E. Sharkey (Eds.), Connectionist approaches to natural language processing (pp. 97-136). Hillsdale, NJ: Erlbaum.
Swanton, C. (1992). Freedom: A coherence theory. Indianapolis: Hackett.
Thagard, P. (1988). Computational philosophy of science. Cambridge, MA: MIT Press/Bradford Books.
Thagard, P. (1989). Explanatory coherence. Behavioral and Brain Sciences , 12 , 435-467.
Thagard, P. (1991). The dinosaur debate: Explanatory coherence and the problem of competing hypotheses. In J. Pollock & R. Cummins (Eds.), Philosophy and AI: Essays at the Interface. (pp. 279-300). Cambridge, Mass.: MIT Press/Bradford Books.
Thagard, P. (1992a). Adversarial problem solving: Modelling an opponent using explanatory coherence. Cognitive Science, 16, 123-149.
Thagard, P. (1992b). Computing coherence. In R. N. Giere (Eds.), Cognitive Models of Science, Minnesota Studies in the Philosophy of Science, vol. 15 (pp. 485-488). Minneapolis: University of Minnesota Press.
Thagard, P. (1992c). Conceptual revolutions. Princeton: Princeton University Press.
Thagard, P. (1993). Computational tractability and conceptual coherence: Why do computer scientists believe that P not= NP? Canadian Journal of Philosophy, 23, 349-364.
Thagard, P. (forthcoming). Ethical coherence. .
Thagard, P. (in press). Probabilistic networks and explanatory coherence. In P. O'Rorke & G. Luger (Eds.), Computing explanations: AI perspectives on abduction Menlo Park, CA: AAAI Press.
Thagard, P., Eliasmith, C., Rusnock, P., & Shelley, C. P. (forthcoming). Epistemic coherence. .
Thagard, P., Holyoak, K., Nelson, G., & Gochfeld, D. (1990). Analog retrieval by constraint satisfaction. Artificial Intelligence, 46, 259-310.
Thagard, P., & Millgram, E. (1995). Inference to the best plan: A coherence theory of decision. In A. Ram & D. B. Leake (Eds.), Goal-driven learning: (pp. 439-454). Cambridge, MA: MIT Press.
Tsang, E. (1993). Foundations of constraint satisfaction. London: Academic Press.
Verbeurgt, K. (in progress) Approximation in AI. Ph. D. thesis, University of Waterloo, Department of Computer Science.